Week 11 Tutorial
Recorded videos (Thanks Willy!)
Graphs
Graphs are used as a model to represent the relationship between the representation of items and problem we need to solve. We are trying to find a different way to represent a problem and use tools to solve it.
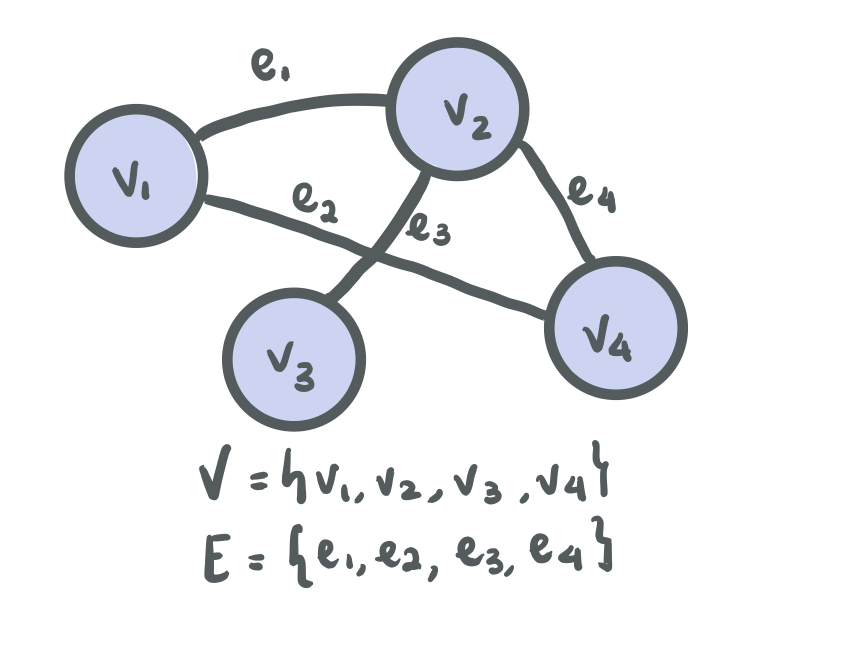
Definition of a Graph
Each graph G = (V,E) consists of:
- A set of nodes that represent data items. We call that set V.
- A set of edges that represent the connections (relationship) between nodes. We call that set E.
Types of Graphs
There are two general types of graphs, undirected and directed
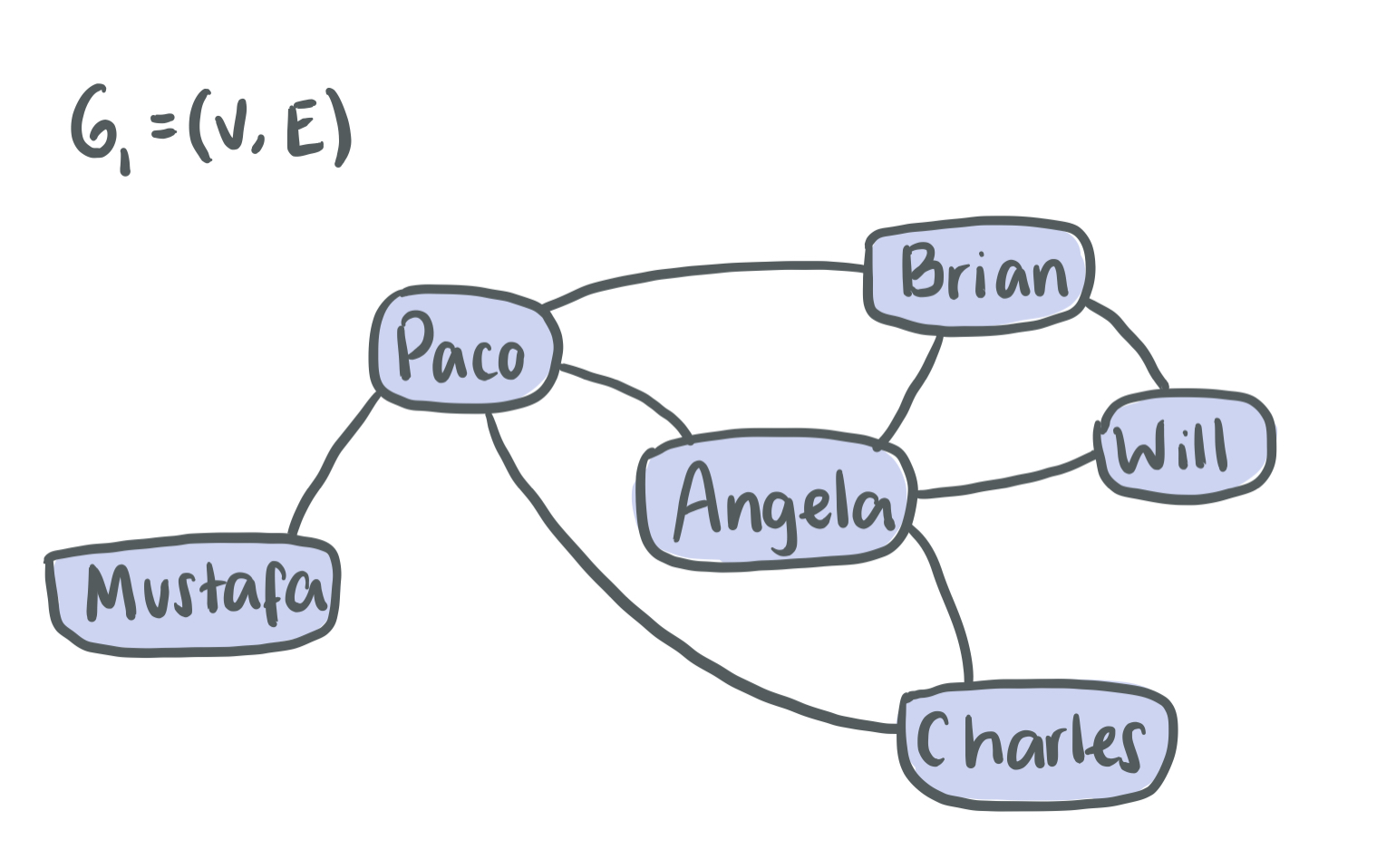
Undirected graphs
Graphs with edges that represent direction in both ways, in other words, there is a reciprocal relationship.
Example: Facebook’s friend network
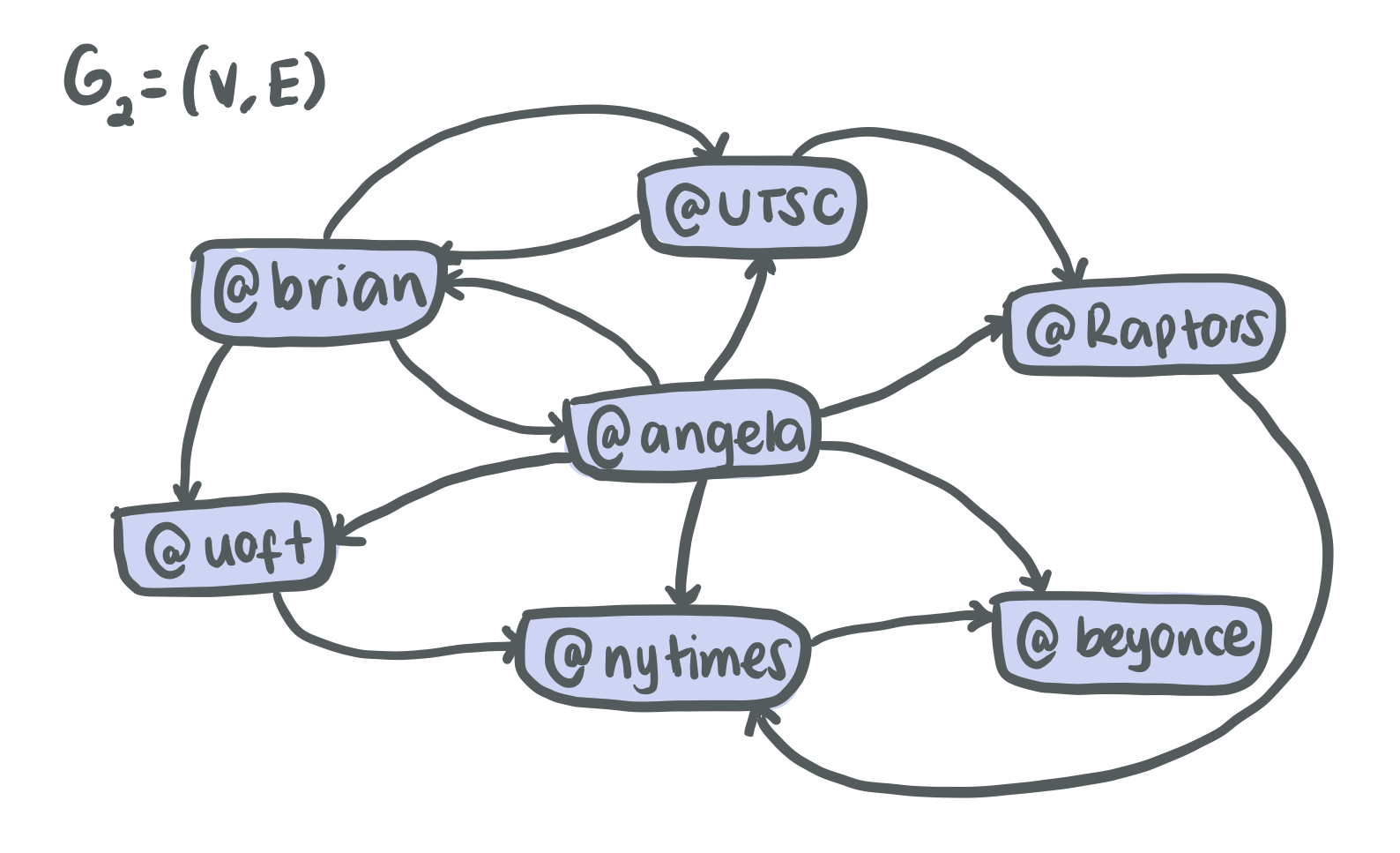
Directed graphs
Graphs with edges that represent one side direction, in other words, there is a one way relationship.
Example: Twitter’s followers network
Terms to remember
Neighbours
For an undirected graph, a node v is a neighbour of the node u if there exists an edge between those two nodes (that edge is represented by {u,v}).
Example: In G1, the neighbour of Mustafa is Paco.
For a directed graph, a node v is a in-neighbour of the node u if there exists an edge {u,v} from u to v. A node v is a out-neighbour of the node u if there exists an edge {v,u} from v to u.
Example: In G2, @Raptors is an in-neighbour of @UTSC, and @UTSC is an out-neightbour of @Raptors.
Neighbourhood
For an undirected graph, the neighbourhood of a node v is the set of all nodes that are neighbours of v.
Example: In G1, the neighbourhood of Charles is the set of nodes {Paco, Angela}.
For a directed graph, there exists an out-neighbourhood and an in-neighbourhood.
Example: In G2, the out-neighbourhood of @Brian is the set of the nodes {@UTSC, @Uoft, @Angela} and the in-neighbourhood of @Brian is the set of the nodes {@UTSC, @Angela}
Degree
For an undirected graph, the degree of a node v is the size (number of nodes) in the neighbourhood of v.
Example: In G1, the degree of Will is 2.
For a directed graph, the node v has an in-degree and an out-degree.
Example: In G2, the out-degree of @nytimes is 1 and the in-degree is 3.
Path
A path is a sequence of consecutive nodes that can be visited by following exisiting edges between each pair of consevutive nodes.
Cycle
For undirected graphs, a cycle is a path with at least three nodes that starts and ends at the same node.
Example: In G1, there is a cycle between the nodes Brian, Will and Angela.
For directed graphs, a cycle is a path that begins and ends at the same node, but in this case the path can have any number of nodes.
Example: In G2, there is a cycle between the nodes @Brian, @UTSC and @Angela.
Exercise
Find the neighbourhood and degree of each node in G1 and G2. Find all cycles in G1 and G2.
Representing Graphs
Adjacency list
The adjacency list is an array of size N with one entry per node, where N is the number of nodes in the grpah. The ith entry of the array contains a pointer to a linked list that stores the indexes of the nodes that i is connected to (the neighbours of i).
Adjacency matrix
The adjacency matrix is a 2D array of size N x N, where N is the number of nodes in the graph. For an undirected graph, the entry A[i][j] is 1 if nodes i and j are connected, and zero otherwise. For a directed graph, the entry A[i][j] is 1 if there is an edge from i to j, and zero otherwise.
Exercise
Represent G1 and G2 using Adjacency lists and matrices.